この問題解けますか？ 第５問

問題（出題者：ｊｐ）
a=b 　　両辺に×a　↓
a2=ab 両辺に＋(a2-２ab) ↓
２a2-２ab=a2-ab （）でくくって簡単に　↓
２(a2-ab)=a2-ab ↓
２=１　
・・・となってしまいます！
あり得ません！何故か説明しなさい！


回答はコメント欄にお願いします。
（回答する場合は”管理者へのみの表示”の設定を行ってください。
これは、まだ問題を解いていない方への配慮です。）

解答発表時に、各々の回答を発表させて頂きます。
また、正解者名の発表も行います。

解答発表予定日：８月６日　８月５日
都合上また発表予定日を変更させていただきます。
どうかご了承下さいませ。

解答編

今日から夏休み

やっと夏期講習前期が終わりました。

今日から夏休みなのですが、宿題の量が半端じゃないんですよ。

英語の宿題なんか、１００ページ近くあるワークブックをやってこいだの・・・

ホントにありえないです；；

まぁ地道にやっていくしかないんですかね？・・・

この問題解けますか？ 第４問解答

---解答---
3/(1+2log510) = 3/(log55+2log510) = 3/(log5500) = log5005^3
log5005^3 = log100ab
logab =  log55^3 = x = 3 （「a,b,xが自然数」の条件に適する）

x^(10x)^x = 3^30^3 = 3^27000  ←の数はN桁なので
10^(N-1)≦3^27000 ＜10^N  ←各辺の常用対数をとると
N-1 ≦ 27000log103 ＜N
N-1 ≦ 12881.7 ＜N　　　N=12882

√√√N = N^(1/8)
6561 ≦ 12882 ＜65536
6561=3^8　　65536=4^8　　12882=N

したがって　√√√Nの整数部分は３である。

答え：３

よろしかったら、この問題ついての感想をコメント欄にお書き込みください。

１人中１人正解

正解者：
（NONAME）

この問題解けますか？ 第４問

指数・対数をしっかり理解していれば解ける問題です。


問題
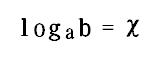（a,b,x は自然数）
上の式において、底の部分を実際の１００倍の値で計算したところ、

x は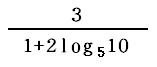という値になってしまった。


正しい x の値で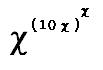という式を作ったとき、

Ｎ桁の数になった。


さて問題、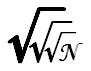の値の整数部分は何になるでしょう。

（回答は答えのみでＯＫです。）


回答はコメント欄にお願いします。
（回答する場合は”管理者へのみの表示”の設定を行ってください。
これは、まだ問題を解いていない方への配慮です。）

解答発表時に、各々の回答を発表させて頂きます。
また、正解者名の発表も行います。

解答発表予定日：８月４日

解答編

この問題解けますか？ 第３問解答

問題
円周率が３．１０より大きいことを証明せよ。

---解答---
半径１の円に内接する正二十四角形があるとき、

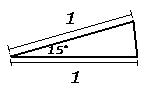
上図のような三角形が２４個あることになる。

加法定理より
sin15°=sin(60°－45°) =sin60°cos45°－ cos60°sin45°
= ｛√（６）－√（２）｝／４

したがって図の三角形の面積は、
１／２　・１・１・　｛√（６）－√（２）｝／４　＝｛√（６）－√（２）｝／８となる。
ゆえに正二十四角形の面積は３｛√（６）－√（２）｝。

√（２） ＜1.41422    √（６）＞2.44948 　なので
√（６）－√（２）　＞1.03526
３｛√（６）－√（２）｝　＞3.10578
円に内接している正二十四角形が３．１０より大きいので
πr^2＞３．１０　　ｒ=1なので
π＞３．１０

したがって円周率は３．１０より大きい。



よろしかったら、この問題ついての感想をコメント欄にお書き込みください。

１人中１人正解

正解者：
くぁｗせｄｒｆｔｇｙふじこｌｐ

この問題解けますか？ 第３問

数学Ⅰ・Ⅱを既習とするレベル

問題

円周率が３．１０より大きいことを証明せよ。

ヒント：正二四角形の面積



この問題は、漫画『ドラゴン桜』で取り上げられた問題をもうちょっと難しくしたものです。
東大の過去問では、円周率が３．０５より大きいことを証明させたそうです。


回答はコメント欄にお願いします。
（回答する場合は”管理者へのみの表示”の設定を行ってください。
これは、まだ問題を解いていない方への配慮です。）

解答発表時に、各々の回答を発表させて頂きます。
また、正解者名の発表も行います。

解答発表予定日：８月３日

解答編

この問題解けますか？ 第２問解答

問題編はこちら


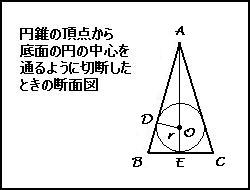
Ⅰ.ⅰ 円錐のにおいて、上図のようにA,B,Cをとり、ＡＢと球の接点をＤ、ＢＣと球の接点をＥ、球の中心をＯ、半径をｒとする。
問題文より、AB=3k  BC=2k （kは比例定数）なので、BE=kである。

ⅱ△ABEと△AODにおいて
∠AEB=∠ADO=90°（円の接線より）、　∠BAE=∠OAD （共通の角）　より、それぞれの２つの角が等しいので △ABE∽△AODとなる。

Ⅱ.ⅠよりAB：BE＝AO：OD、　よって3k：k＝｛2√(2)k－ｒ｝：ｒなので、
3kr=2√(2)k^2 －kr
3r=2√(2)k－ｒ
4r=2√(2)k
r=k/√(2)となる。

Ⅲ.円錐の表面積において

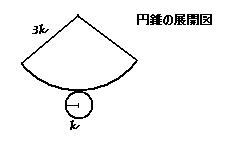
底面部分の面積はk^2 π。
扇形の弧の長さは2kπであるから、この扇形は半径3kの円の 1/3の大きさとわかる。
したがって、扇形の面積は 1/3 ・ 9k^2 π =3k^2 π。
よって円錐の表面積は 4k^2 πとなる。

Ⅵ.球の表面積において
Ⅱより、球の半径が k/√(2) なので、表面積は 4πr^2 = 4π ・ k^2 / 2 =2k^2 πとなる。


以上のことより、円錐と球の表面積の比は 4k^2 π ： 2k^2 π　＝２：１。

答え：　円錐の表面積：球の表面積＝２：１

よろしかったら、この問題ついての感想をコメント欄にお書き込みください。

４人中１人正解

正解者：
くぁｗせｄｒｆｔｇｙふじこｌｐ