Sphere 綺麗な絵の脱出ゲーム

□Sphere　綺麗な絵の脱出ゲーム

●綺麗な絵の脱出ゲームです。
さらに、驚くべきことに「セーブ機能」付きなんですよ＾＾

ちなみに、使うのはマウスのみです。

---

この記事が「面白かった」「よかった」と思った人は、
↓クリックよろしくお願い致します。
（ブログランキングに反映されますので）
　　

この問題解けますか？ 第２問解答

問題編はこちら


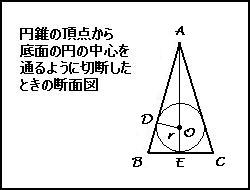
Ⅰ.ⅰ 円錐のにおいて、上図のようにA,B,Cをとり、ＡＢと球の接点をＤ、ＢＣと球の接点をＥ、球の中心をＯ、半径をｒとする。
問題文より、AB=3k  BC=2k （kは比例定数）なので、BE=kである。

ⅱ△ABEと△AODにおいて
∠AEB=∠ADO=90°（円の接線より）、　∠BAE=∠OAD （共通の角）　より、それぞれの２つの角が等しいので △ABE∽△AODとなる。

Ⅱ.ⅠよりAB：BE＝AO：OD、　よって3k：k＝｛2√(2)k－ｒ｝：ｒなので、
3kr=2√(2)k^2 －kr
3r=2√(2)k－ｒ
4r=2√(2)k
r=k/√(2)となる。

Ⅲ.円錐の表面積において

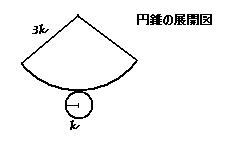
底面部分の面積はk^2 π。
扇形の弧の長さは2kπであるから、この扇形は半径3kの円の 1/3の大きさとわかる。
したがって、扇形の面積は 1/3 ・ 9k^2 π =3k^2 π。
よって円錐の表面積は 4k^2 πとなる。

Ⅵ.球の表面積において
Ⅱより、球の半径が k/√(2) なので、表面積は 4πr^2 = 4π ・ k^2 / 2 =2k^2 πとなる。


以上のことより、円錐と球の表面積の比は 4k^2 π ： 2k^2 π　＝２：１。

答え：　円錐の表面積：球の表面積＝２：１

よろしかったら、この問題ついての感想をコメント欄にお書き込みください。

４人中１人正解

正解者：
くぁｗせｄｒｆｔｇｙふじこｌｐ

この問題解けますか？ 第２問

去年、私が高校１年生のころに作った問題を見つけたので、発表させていただきます。
今回は、前回の問題に比べて簡単なものとなっています。

数学に自信のある方は、解いてみてください。
（数学Ⅰを既習とするレベルとなっています）


問題

上図のように、円錐に内接する球がある。
円錐の底面の直径と母線の比が２：３のとき、
円錐と球の表面積の比を求めよ。


回答はコメント欄にお願いします。
（回答する場合は”管理者へのみの表示”の設定を行ってください。
これは、まだ問題を解いていない方への配慮です。）

解答発表時に、各々の回答を発表させて頂きます。
また、正解者名の発表も行います。

解答発表予定日：７月２９日

解答編はこちら

---

この記事が「面白かった」「よかった」と思った人は、
↓クリックよろしくお願い致します。
（ブログランキングに反映されますので）
　　

ここはゲームを紹介するところなのに・・・

すみませんね。

昨日今日いきなり数学の話持ち出しちゃって・・・

でも、ホントに数学が好きで好きでたまらないんですよ＾＾；；

また時間があったら　また問題発表したいと思います。
（アクセス数も倍に上がっちゃってるし・・・）



明日からまた普通どおりゲームの紹介記事を書いていきますので、

心配しないでくださいね。

この問題解ける方いますか？ 解答編

問題編はこちら


BP=3  RS=4  BC⊥QP

-----解答-----
Ⅰ.△ABPと△APCの面積比は１：４。
この２つの三角形は高さが同じなので、底辺の長さの比が１：４となる。
したがってＰＣ＝１２。

△PQRと△QRSの面積比は１：２。
この２つの三角形も高さが同じなので、底辺の長さの比が１：２となる。
したがってPR=4  RC=8。

Ⅱ.△PQRと△SQRにおいて
ⅰ. Ⅰより、ＰＲ=SR=４　QR=QR（共通）　面積が等しい　ので
△PQRの面積は　（1/2）・PR・QR・sin∠PRQ
△SQRの面積は　（1/2）・SR・QR・sin∠SRQ
よって、（1/2）・PR・QR・sin∠PRQ＝（1/2）・SR・QR・sin∠SRQ。
ゆえに、sin∠PRQ=sin∠SRQ……①

ⅱ. このとき∠PRQ＋∠SRQ＜１８０°……②（SはRC上にあってはならないことより）
∠PRQ＜９０°（BC⊥QPの∠QPR=９０°より）　なので、
∠SRQ＜９０°のときと　　９０°＜∠SRQ＜１８０°の場合が考えられる。

ⅲ. しかし、９０°＜∠SRQ＜１８０°の場合、
①式より、∠SRQ＝　（１８０°－∠PRQ）となる。
これは、∠PRQ＋∠SRQ＝１８０°となってしまい、②式に矛盾するので、
９０°＜∠SRQ＜１８０°は成り立たない。
したがって∠SRQ＜９０°となり、∠PRQ=∠SRQとなる。

ⅳ. △PQRと△SQRにおいて
２辺とその間の角が等しいので、△PQR≡△SQR。

以上のことより、∠RSC=９０°

Ⅲ.△SRCにおいて
RS=4  RC=8　より、cos∠SRC=1/2
したがって、∠SRC=６０°、sin∠SRC=√(3) /2　となる。
△SRCの面積は、（1/2）・SR・RC・sin∠SRC=8√(3)……③


③式より、△ABCの面積を５等分したものの面積が8√(3) なので、
△ABCの面積は、5・8√(3)＝４０√(3)　となる。

答え：４０√(3)


よろしかったら、この問題ついての感想をコメント欄にお書き込みください。

正解者：
Schwarz

計１名

この問題解ける方いますか？

私実は趣味が「数学研究」なんです。


一体どんなことをする趣味なのか？

というのは、学校で教えないような問題を解いてみたり、作ってみたりするんです。

とても数学が好きな人にしか、その面白さはわからないと思いますが・・・・・・


今日は、思い切って私が作った問題を発表したいと思います。

ちなみに、問題は高１レベル（三角比を既習とする）となっています。


問題

△ABCがある。
上図のように、△ABCの面積を５等分するように、線分AP,PQ,QR,RSを引いた。
ＢＰ=３　ＲＳ=４　ＢＣ⊥ＱＰ　のとき、△ABCの面積を求めよ。


回答はコメント欄にでも。
解答は今週日曜日に発表します。

すみません。
こちらの都合上、7/26に解答を発表させていただきます。
ご了承くださいませ。

解答編はこちら

BUM BUM KOALA カタツムリをやっつけろ！

□BUM BUM KOALA　カタツムリをやっつけろ！

情報提供：くろ

●コアラがカタツムリを落としていくゲームです。
コアラの大きさに比べると、カタツムリのあまりの大きさに笑ってしまいますが、これがゲームの面白さなのでしょうね＾＾；

ＢＧＭもゆったりした音楽で、私は気に入りましたね＾＾
これも、一種の癒しゲームなのかもしれません。

---

この記事が「面白かった」「よかった」と思った人は、
↓クリックよろしくお願い致します。
（ブログランキングに反映されますので）